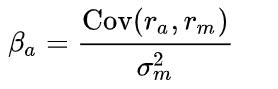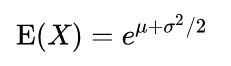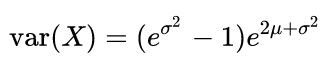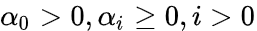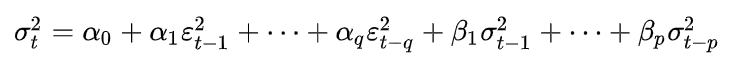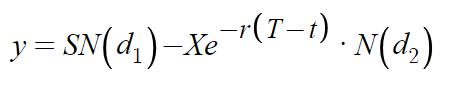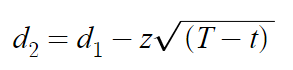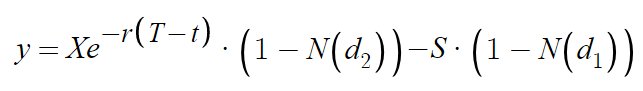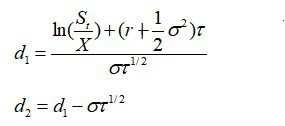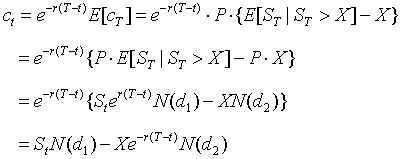摘要:随着期权交易的发展,市场上有形资产和无形资产的期权交易成为可能,期权的价值估定问题亟待解决,下面本文就概率论在研究期权价值的估定方面做出阐释。
关键词:概率论,期权,定价,应用
Application of Probability Theory to Option Pricing
Abstract: With the development of option trading, option trading of tangible and intangible assets in the market has become possible, and the problem of valuation of options needs to be solved.
Keywords: probability theory, options, pricing, applications
1.Black-Scholes模型概述
1.1 期权定价理论的由来
期权是指买方支付一定的期权费用后,在未来允许的时间内购买或出售一定数量的基础商品。期权定价是期权交易的核心问题,它直接影响到买卖双方的盈亏。早在1900年,法国金融专家劳雷斯·巴舍利耶发表了第一篇关于期权定价的文章。此后,各种经验公式、计量定价模型相继出现,但由于种种局限性,难以得到普遍认同。上世纪70年代以来,随着期权市场的迅速发展,期权定价理论研究取得了突破性进展。
国际衍生品市场的形成与发展过程中,如何合理定价一直是投资者面临的一个难题。计算机与先进通信技术的应用使得复杂期权定价公式成为可能。在将近50年的时间里,投资者利用布莱克-斯克尔斯期权定价模型将这个抽象的数字公式转化为财富。费雪·布莱克和默顿在巴施里耶,斯普伦克莱,博内斯,萨缪尔森等人的研究基础上,开发了期权定价模型,并得到广泛应用。1979年,约翰考克斯、斯蒂芬· A·罗斯、马克·鲁宾斯坦等人以费雪、默顿的工作为基础,完成了一篇名为期权定价数值法奠定基础的论文《期权定价:简化方法》。
1.2 Black-Scholes期权定价理论的基本假设
基本假设分为七点,1.在期权运行周期内,标的资产波动率不变。公式的核心是假设资产价格下一个变动幅度是可知的,但方向不确定。资产价格变化不会出现跳跃,2.在期权的有效期内,无风险利率和资产收益恒定,3.市场无摩擦,无交易手续费,标的资产可以拆分交易,4.该期权是欧式期权,5.不存在无风险套利机会,6.交易是持续不间断的,7.投资者能以无风险利率借贷。
1.3期权定价中的希腊字母[1]
Delta值:期权价格和资产价格之间的变化率。持有一份Delta值为1的看涨合约意味着一份标的的价格风险敞口所对应的风险价值。
Gamma值:Delta值和标的价格之间的变化率。期权价格变化相对于标的资产价格变化敏感程度的二阶导数。
Gamma值高表明即使标的的价格变动很小,Delta值也可能发生很大变化。而Gamma值低则表明相反的情况。
隐含波动率(IV):IV反映了市场对标的未来波动的预期。
IV值高表明市场预期标的价格将有较大波动(并且期权价值将上升),而相反,IV值低则反映了较小的波动预期。波动率为收益率的标准差。
Theta值:衡量期权价值随时间的损耗速度,也称为时间价值衰减。
Beta系数是一种评估系统风险的工具,用来衡量标的相对于整个市场的波动性。
其中,Cov(ra,rm)是标的a的收益与市场收益的协方差,σ2m是市场收益的方差。贝塔系数利用回归的方法计算:若其绝对值高于1,则表明该标的比市场平均波动为大,等于1则随市场一同波动,小于1则表明该标的比市场平均波动为小。
β值用于衡量该标的的系统性风险,计算方式是用过去12个月或者24个月该标的的月回报率对同期市场月回报率做回归分析,从而估算出其斜率系数。尽管在期权交易中不直接使用Beta参数,但可以用它衡量标的的风险情况,标的的风险会影响相关期权合约的隐含波动率。
1.4 对数正态分布
由于标的现货交易价格一般不会为负数,所以我们在期权交易时一般使用对数正态分布模型,当一个变量可以看成是若干个很小的独立因子的乘积时,它就可以被视为一个对数正态分布。其公式如下: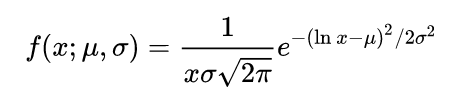
1.5布朗运动与一般维纳过程
鞅是一种满足以下条件的随机过程:已知过去某时刻 s和之前所有时刻的观测值,如果某时刻 t观测值的条件期望等于过去某时刻 s的观测值,则称为鞅。Mt是一个布朗运动当且仅当为Mt为鞅,且M2t-t也为鞅.随机过程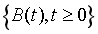 称为布朗运动(维纳过程),如果它满足:(1)过程具有独立增量;(2)正态增量,即
称为布朗运动(维纳过程),如果它满足:(1)过程具有独立增量;(2)正态增量,即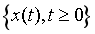 ;(3)是一个连续函数。
;(3)是一个连续函数。
设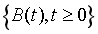 为布朗运动,则称
为布朗运动,则称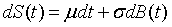 为一般化的维纳过程(布朗运动)。称μ为瞬时期望漂移率,σ为瞬时标准差,它们都是给定的参数,B(t)是连续的维纳过程。
为一般化的维纳过程(布朗运动)。称μ为瞬时期望漂移率,σ为瞬时标准差,它们都是给定的参数,B(t)是连续的维纳过程。
如果我们不计算ΔB在内,则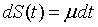 ,
,
即 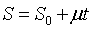 ,这说明资产价格具有线性增长的性质。如果我们考虑ΔB,这种波动分为两个部分,(1)dB,即所谓白噪声(white noise),(2)它被放大了σ倍,则有
,这说明资产价格具有线性增长的性质。如果我们考虑ΔB,这种波动分为两个部分,(1)dB,即所谓白噪声(white noise),(2)它被放大了σ倍,则有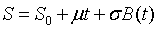 ,这说明资产价格 S具有随机波动的趋势,同时线性增长,两者相加,得到了一般的维纳过程。
,这说明资产价格 S具有随机波动的趋势,同时线性增长,两者相加,得到了一般的维纳过程。
1.6几何布朗运动
对于一般金融资产而言,瞬时预期回报率μ与回报率标准差σ可能并非常数,而是某一金融资产价格与时间之函数,即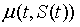 与
与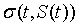 之相加,因此该金融资产的价格变化规律由下式表示:
之相加,因此该金融资产的价格变化规律由下式表示:
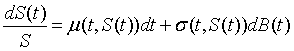
1.7 伊藤过程
如果过程{S(t),0<=t<=T}可以表示为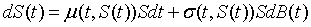 ,
,
其中μ(t,s),σ(t,s)是二元连续函数,{B(t),t>=0}为布朗运动,则称{S(t),0<=t<=T}为伊藤过程。
伊藤定理:
设{S(t),0<=t<=T}是由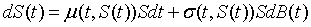 给出的伊藤过程,f=f(s,t)是二次可微连续函数,具有连续偏导数:
给出的伊藤过程,f=f(s,t)是二次可微连续函数,具有连续偏导数: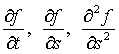
则f(S(t),t)满足如下的伊藤微分方程: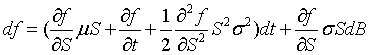
由于资产价格定价服从伊藤过程,所以根据伊藤定理,在给定当前资产价格的情况下,未来的资产价格服从对数正态分布(见1.4).
1.8 预测波动率的基本模型
1.8.1 GARCH模型[2]
若用ARMA模型来表示方差,则GARCH模型是ARCH模型的改进。
ARCH模型的基本公式如下:以ε表示收益或收益残差,假设εt=σtzt,此处zt服从独立同分布,即均符合期望为0,方差为1的正态分布,在这里序列σ2t被建模为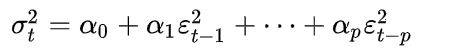
传统计量经济学中关于时间序列变量的第二种假设:假设时间序列中的变量的振幅(方差)是固定的,与现实不符,例如,长期以来,人们已经发现,股价的涨落会随着时间的推移而改变,并且是变量。这就导致了传统的时序分析方法无法解决实际问题。
1.9 波动率的变化原理以及对市场的影响
对期权价格影响最大的因素并非标的价格方向,而是对标的市场价格变化的快慢程度的感知。如果市场变动非常迅速,那么所有期权的价值就会增加,不管是看涨期权还是看跌期权,不管是行权价格高还是行权价格低。同样,如果市场非常缓慢地变动,那么所有的期权价值又将如何变化呢?不管是看涨期权还是看跌期权,不管是行权价高还是行权价低,它们都会大幅下跌。这就是期权市场的独特之处:相对于标的市场的变动方向而言,期权市场对标的市场变动速度的影响更为显著。
预测长期波动率比预测短期波动率更容易。
我们通常会想到,随着周期的延长,不确定性会越来越大。但在波动率方面,却恰恰相反。虽然并不绝对,其曲线类似于一条移动平均线,随着时间的推移,它的移动平均线会变得更加的平稳,而它的曲线也会变得更加的光滑。波动率也大致如此。
总体上讲,波动率具有三个特点:
序列相关性——在没有其它数据的时候,对后期波动率的最佳预测是与前期波动率情况相同。
均值回归——在给定了过往的波动性资料后,最好的预测就是波动性会回到其历史平均水平。
动量效应——当波动性已经显示出某种趋势时,最好的预测就是这种趋势会持续下去。
1.10 Black-Scholes期权定价理论的基本公式
在此公式中,S是标的的价格,N(x)是x的累计标准正态分布,r是无风险收益率,X为期权行权价格,T为期权到期时间,t为当前时间。z为期权波动率。其中d1,d2为: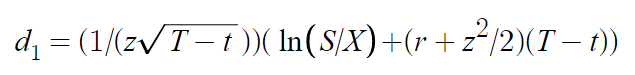
1.11 Black-Scholes期权定价理论的基本公式的推导
随机过程的一个分支——随机微分方程和鞅是期权定价的重要工具。日本数学家伊藤清在研究马尔可夫过程的内在机制时,提出布朗运动(也称为维纳过程)是一种最基础的扩散过程,可以利用其进行一般的扩散的计算。
如果是欧式买权,且现在时刻t距到期日期 T还有一段时间,那么,就不能用目前市场价格S减去执行价格X作为其固有价值,因为这是两个不同时刻发生的价值,如果从资金的时间价值角度来看,单纯的计算加减没有任何意义,应该把 T时刻的价值 X以无风险利率 r贴现至目前时刻。因此,欧式买权内在价值的计算公式应当调整为 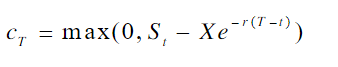
Black-Scholes考察一类特殊的扩散过程: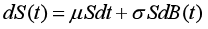 ,这里St表示标的价格,标的预期收益率μ及波动率σ(σ≠0)均为常数,t代表时间,B(t)为标准布朗运动。在无交易成本、没有分红的假设下,得出欧式看涨期权价格Ft应满足如下微分方程 (r为无风险利率 ):
,这里St表示标的价格,标的预期收益率μ及波动率σ(σ≠0)均为常数,t代表时间,B(t)为标准布朗运动。在无交易成本、没有分红的假设下,得出欧式看涨期权价格Ft应满足如下微分方程 (r为无风险利率 ):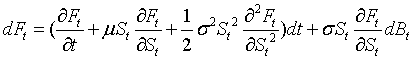
利用偏微分方程的理论求出的方程解析解 ,即著名的Black-Scholes期权定价公式。(见1.10)
1.12 Black-Scholes期权定价理论的风险中性定价解法[3]
风险中性指的是:风险中性者对风险的态度是漠不关心的:无论风险如何,他们对所有资产的预期收益率都是相同的,不会要求补偿风险。因此,要求所有资产的预期收益率与无风险资产的收益率是一样的。也就是说,风险中性投资者对任何资产的投资要求都是无风险收益率。
设P为达到盈利的概率。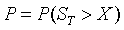
则 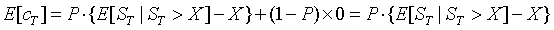
由单调函数的性质:P满足 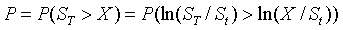
在模型里,由于满足风险中性学说,所有资产的预期收益等,均等于无风险收益率r,即μ=r。因此,由模型假设知,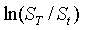 服从正态分布,其期望值和方差分别为:
服从正态分布,其期望值和方差分别为:
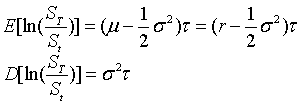
其中,τ=T-t ,换元,
令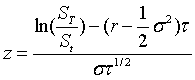
则可以化作标准正态分布形式,有 z ~ N(0,1)
因此,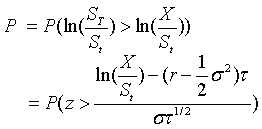
则上式为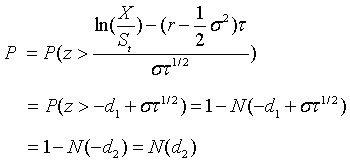
这样,我们求出了第一个值。
由于 ,服从对数正态分布,因此其密度函数
,服从对数正态分布,因此其密度函数
为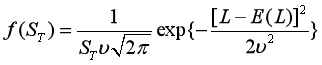
其中,
于是:
作变量替换
则有
计算积分限,当  时,
时, ;当ST=X时,
;当ST=X时,

因此,
至此, 和
和 均已求出,则该期权价值
均已求出,则该期权价值
即为所求,解毕。
2.结论
本文介绍了期权定价理论的由来,并运用随机过程知识对欧式期权定价进行了系统的研究。本文对标的资产的价格过程进行了推导,并运用风险中性法对布莱克-斯科尔斯模型进行了详细的分析。
参考文献
[1] (美)谢尔登·纳坦恩伯格,期权波动率交易策略.机械工业出版社,2014年9月
[2] (英)特里·J.沃特沙姆,基思·帕拉莫尔.陈工孟,陈守东译.金融数量方法.上海人民出版社,2004年05月.
[3] 基于Black-Scholes模型的欧式期权定价研究.高皓,束为,2004年